目前主流的定位感知技术

从技术角度讲，分为基于信号强度的三角定位，基于无线电波的相角定位技术，AOA，AOD，DOA,TDOA，等定位技术。 例如 GPS 采用的是 DOA 定位原理。 而今天重点讲最新型技术 AOA/AOD 定位探索。

让我们考虑一个带有多天线线性阵列的设备用于接收器和一个带有一个天线的设备用于发射器。此外，假设无线电波作为平面波前传播而不是球形，我们可以 安全地从远处观察。如果通过空气发送正弦波的发射器位于垂直于阵列线的法线上，则阵列的每个天线(信道)将看到相同相位的输入信号。如果发射器不在 法线上，则接收天线将看到信道之间的相位差。该相位差信息可用于计算到达角。

实际上，接收器需要具有多个 ADC 通道或使用 RF 开关从每个单独的通道采集样本。这些样本称为“IQ 样本”，因为一对“同相”和“正交相位”读数取自相同的输入 信号。这些样品在采样中具有 90 度的相位差。当该对被认为是复数值时，每个复数值包含相位和幅度信息，并且可以是到达角估计算法的输入。

无线电波以 300,000km / s 的光速传播。当使用 2.4GHz 左右的频率时，相应的波长约为 0.125m。对于大多数估计算法，两个相邻天线之间的最大距离是半波 长。许多算法都需要这个，否则我们会得到类似于别名的效果。没有理论上的最小距离限制，但在实践中，最小尺寸受到阵列的机械尺寸以及例如天线元件之 间的相互耦合的限制。

对于离开角度，测量相位差的基本思想是相同的，但设备角色是交换的。在 AoD 中，被跟踪的设备仅使用一个天线，并且发射机设备使用多个天线。发送器设 备顺序地切换发送天线，并且接收侧知道天线阵列配置和切换序列。

从应用的角度考虑这一点时，我们可以看到这两种技术之间存在明显差异。在 AoD 中，接收设备能够使用来自多个信标的角度及其位置(通过三角测量)计算 其自身在空间中的位置。在 AoA 中，接收设备跟踪各个对象的到达角度。但是，值得注意的是，可以执行这些的不同组合; 因此，这些技术不限制在应用程序 级别可以执行的操作。在蓝牙 AoA 和 AoD 中，相关的控制数据都通过传统的数据信道发送。通常，这些技术可以实现几度角度精度和约 0.5 米定位精度，但是 这些数字高度依赖于定位系统的实现。

角度估计方法和天线阵列对于定位系统正常工作至关重要。定向探测理论的历史可以追溯到 100 多年前，当时第一次使用定向天线和显然纯模拟系统来解决这 个问题。在接下来的几年里，测试方法转移到了数字世界，但基本原理仍然非常相似。这些测向方法已经在许多应用中使用，例如医疗设备，安全和军事设 备。在本节中，我们将讨论一些典型天线阵列和估算算法的基础知识。通过测向，我们参考估计到达和离开角度的一般问题。

用于测向的天线阵列通常分为几类。这里讨论的最常见的是均匀线性阵列(ULA)，均匀矩形阵列(URA)和均匀圆阵列(UCA)。线性阵列是一维阵列，意 味着阵列中的所有天线都位于一条线上，而矩形和圆形阵列是二维阵列，这意味着天线分布在两个维度上(在一个平面上) 。通过使用一维天线阵列，假设被 跟踪设备在同一平面上一致地移动，则可以可靠地仅测量方位角。此外，利用二维阵列，可以可靠地测量 3D 半空间中的方位角和仰角。如果阵列扩展到完整 的 3D 阵列(天线分布在所有三个笛卡尔坐标上)，然后我们将能够测量完整的 3D 空间。设计用于测向的天线阵列不是一项简单的任务。

在物联网应用中，通常期望这些设备很小，甚至可以在非常高的频带中工作。估计算法通常需要阵列中的某些特性。例如，称为 ESPRIT 的估计算法基于数学假 设，该数组被分成两个相同的子阵列[3]。当天线放置在阵列中时，它们开始影响彼此的响应;这称为互耦。我们还必须记住，在大多数情况下，我们无法控制发 射端的极化。这给我们带来了额外的挑战。

让我们看看基于输入 IQ 数据估计到达角的数学/算法问题。问题定义本身很简单:估计到达接收阵列的发射(窄带)信号的到达角。虽然问题陈述听起来非常 微不足道，但对于这个问题而言，一个强大的解决方案(在现实生活中工作)并不容易，并且可能需要来自硬件的大量处理能力。接下来，我们将介绍两种不 同的方法来解决这个问题。第一个是基本的，称为经典波束形成器。第二种是更先进的技术，称为多信号分类(MUSIC)。

让我们从均匀线性阵列的数学模型开始。我们给出了每个天线的 IQ 样本的数据向量。让这个向量称为 x。现在，在测量中，每个天线(可以是 0)加上一些噪 声n可以看到相移，因此x可以写成时间的函数t:

其中s是通过空中发送的信号，a是天线阵列的导向矢量:

其中d是相邻天线之间的距离; λ 是信号的波长; m是天线阵列中的元素数量，θ 代表到达角度。转向矢量(2)描述了由于到发射机的距离变化，每个天线上的信 号如何相移。通过使用(1)，我们可以通过计算计算所谓的样本协方差矩阵Rxx 的近似值

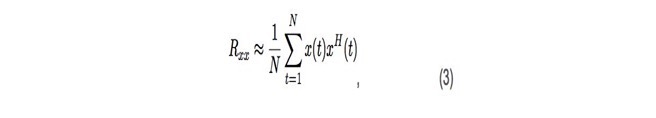
其中 H 代表矩阵的 Hermitian 转置。 如我们将看到的，样本协方差矩阵(3)将用作估计算法的输入。 经典波束形成器的想法是最大化输出功率作为角度的函数，类似于机械雷达的工作方式。如果我们试图最大化功率，我们最终得到下一个公式:

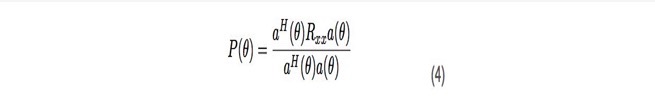
现在，为了找到到达角，我们需要遍历到达角 θ 并找到峰值最大功率𝑃。产生最大功率的角度 ortheta 对应于到达角度。虽然这种方法非常简单，但其准确性通 常不是很好。因此，让我们介绍另一种方法，它在准确性方面要好一些。例如，参见[4]进行算法精度比较。 一种估计算法是所谓的子空间估计器，该类别的一种流行算法称为 MUSIC(多信号分类)。该算法的思想是在协方差矩阵Rxx 上执行特征分解:

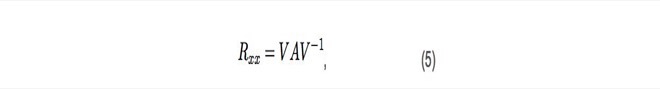
其中A是包含特征值的对角矩阵，V包含Rxx 的相应特征向量。

假设我们正在尝试使用n天线线性阵列估计一个发射机的到达角。可以看出，Rxx 的特征向量或者属于所谓的噪声子空间或信号子空间。如果特征值按升序排 序，则相应的n - 1 特征向量跨越噪声子空间，该子空间与信号子空间正交。基于正交信息，我们可以计算伪谱p:

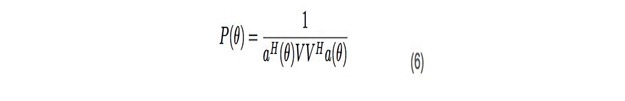
在经典波束形成器中，我们遍历期望的 θ 值并找到 maximum 的最大峰值，其对应于我们希望测量的到达角(参数 θ)。

在理想情况下，MUSIC 在良好的 SNR 环境中具有出色的分辨率，并且非常准确。另一方面，当输入信号高度相关时，其性能不是很强，特别是在室内环境中。 多径效应使伪谱失真，导致其在错误的位置具有最大值。有关传统波束形成器和 MUSIC 估计器的更多信息可以在[3]中找到。

空间平滑是一种解决多路径引起的问题的方法(当存在相干信号时)。可以证明，通过使用原始协方差矩阵的子阵列计算平均协方差矩阵，可以使信号协方差 矩阵“去相关”。对于二维数组，可以写成如下

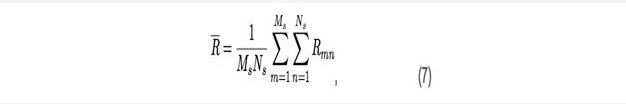
其中M2 和N2 分别是 x 和 y 方向上的子阵列数，Rmm代表(m，n):子阵列协方差矩阵。可以从[2]中找到该公式的示例证明和更多信息。得到的协方差矩阵 现在可以用作协方差矩阵的“去相关”版本，并馈送到 MUSIC 算法以产生正确的结果。空间平滑的缺点是它减小了协方差矩阵的大小，这进一步降低了估计的准 确性。

蓝牙到达角度和出发角度是新兴技术，可用于跟踪资产以及室内定位和寻路。这些是基于相位的测向系统，需要天线阵列，RF 开关(或多通道 ADC)和处理能 力来运行估计算法。设计合适的天线阵列以及角度估计算法对于 RTLS 系统至关重要。强大的性能估计算法通常在计算上不便宜。其他定位技术包括(但不限 于)基于 RSSI 的方法和基于 ToA 的方法，但是仅基于相位的 AoA / AoD 当前在蓝牙中具有标准化框架。

随着新型技术变化的日新月异，灵思科电子科技始终致力于前沿科技，在国内 2019 年首家推出达到 cm 级别的定位精度的定位标签。